傅里叶变换的初级理解三
本文共 899 字,大约阅读时间需要 2 分钟。
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的;
在这个世界上,有的事情一期一会,永不再来,并且时间始终不曾停息地将那些刻骨铭心的往昔连续的标记在时间点上。但是这些事情往往又成为了我们格外宝贵的回忆,在我们大脑里隔一段时间就会周期性的蹦出来一下,可惜这些回忆都是零散的片段,往往只有最幸福的回忆,而平淡的回忆则逐渐被我们忘却。因为,往昔是一个连续的非周期信号,而回忆是一个周期离散信号。 是否有一种数学工具将连续非周期信号变换为周期离散信号呢?抱歉,真没有。比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数;
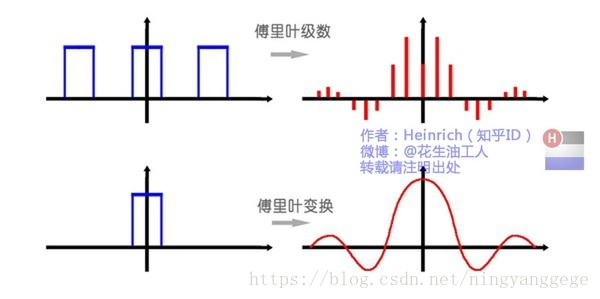
傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号;如图所示:
前面部分是将周期信号转换成傅里叶级数;后面部分将非周期信号转换成频域非周期的连续信号;
或者我们也可以换一个角度理解:傅里叶变换实际上是对一个周期无限大的函数进行傅里叶变换。
所以说,钢琴谱其实并非一个连续的频谱,而是很多在时间上离散的频率,但是这样的一个贴切的比喻真的是很难找出第二个来了。因此在傅里叶变换在频域上就从离散谱变成了连续谱。那么连续谱是什么样子呢?你见过大海么?为了方便大家对比,我们这次从另一个角度来看频谱,还是傅里叶级数中用到最多的那幅图,我们从频率较高的方向看。
 以上是离散谱,那么连续谱是什么样子呢? 尽情的发挥你的想象,想象这些离散的正弦波离得越来越近,逐渐变得连续…… 直到变得像波涛起伏的大海
以上是离散谱,那么连续谱是什么样子呢? 尽情的发挥你的想象,想象这些离散的正弦波离得越来越近,逐渐变得连续…… 直到变得像波涛起伏的大海 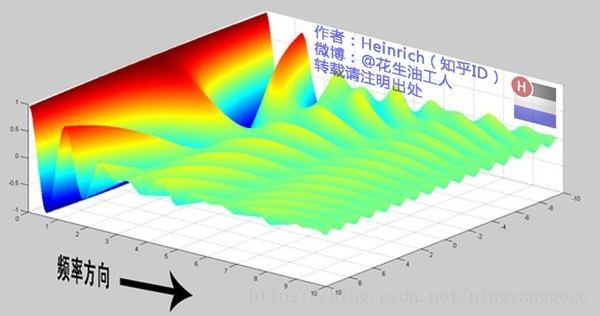 很抱歉,为了能让这些波浪更清晰的看到,我没有选用正确的计算参数,而是选择了一些让图片更美观的参数,不然这图看起来就像屎一样了。 不过通过这样两幅图去比较,大家应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。 不过,这个故事还没有讲完,接下去,我保证让你看到一幅比上图更美丽壮观的图片,但是这里需要介绍到一个数学工具才能然故事继续,这个工具就是——欧拉公式 参考:http://blog.jobbole.com/70549/
很抱歉,为了能让这些波浪更清晰的看到,我没有选用正确的计算参数,而是选择了一些让图片更美观的参数,不然这图看起来就像屎一样了。 不过通过这样两幅图去比较,大家应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。 不过,这个故事还没有讲完,接下去,我保证让你看到一幅比上图更美丽壮观的图片,但是这里需要介绍到一个数学工具才能然故事继续,这个工具就是——欧拉公式 参考:http://blog.jobbole.com/70549/
你可能感兴趣的文章
CentOS下Nvidia docker 2.0之安裝教程&踩坑實錄
查看>>
PIL及matplotlib:OSError: cannot identify image file錯誤及解決方式
查看>>
H5页面授权获取微信授权(openId,微信nickname等信息)
查看>>
SpringBoot的URL是如何拼接的
查看>>
2018年年终总结
查看>>
解决checkbox未选中不传递value的多种方法
查看>>
【pgsql-参数详解1】PostgreSQL默认参数值
查看>>
PostgreSQL11-Hash哈希分区数量的设定标准
查看>>
HTTP协议(1)_入门的一些教程和资源
查看>>
2021年春季ACM训练赛第3场
查看>>
Go-常用命令go的使用(build、env、run、fmt等)
查看>>
钉钉登录及常用的URL及IP
查看>>
CENTOS 删除nginx
查看>>
【redis键过期删除策略】很高兴再次认识你
查看>>
【工具篇】EasyExcel的应用
查看>>
SSM发送手机验证码——以网建SMS为例
查看>>
大范围卫星影像快速处理
查看>>
监控264后缀文件播放
查看>>
Java并发编程笔记-思维导图
查看>>
网站在线偷拍照片源码
查看>>